| PM96: May 2010 |
 | For p a prime number and n an integer that is larger than p but not divisible by p – 1,define 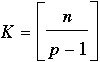 . In words, K is the number of times p – 1 goes into n: . In words, K is the number of times p – 1 goes into n:
n = (p – 1)K + r, with 0 < r < p – 1.
Prove that
is divisible by p. |
 Solution. Solution.
|
| PM95: April 2010 |
 | What can you say about the angles of a triangle having the property that when you divide the sum of the cubes of the sides by its perimeter, you get the area of the square on one of its sides?
|
 Solution. Solution.
|
| PM94: March 2010 |
 | Here is a 3-part problem for month number 3:
- Can you find integers s and t, both greater than 1, for which (ss)2 = tt?
- Can you find integers s and t, both greater than 1, for which ( ss)2010 = tt?
- Can you find integers s and t, both greater than 1, for which s(s2010) = tt?
|
 Solution. Solution.
|
| PM93: February 2010 |
 | The eleven members of the local football team gather at the pub after each game. Afterwards, they roll a pair of dice to determine who picks up the tab. Happily, the numbers on their jerseys run from 2 to 12, so the player whose jersey number matches the sum that shows on the dice pays the bill. But even a football player realizes that the eleven sums are not equally likely. Your task this month is to help make the process fair:
Describe how to load a pair of dice, one red, one green, so that every sum from 2 to 12 is equally likely, or prove that it is impossible.
|
 Solution. Solution.
|
| PM92: January 2010 |
 | Show that the product
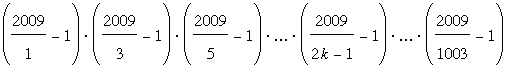
is a power of 2. |
 Solution. Solution.
|
| PM91:December 2009 |
 |
 |
| stamp-search.com | |
Snow White married the prince and lived happily ever after. Eventually the mine closed and the seven dwarfs went into retirement, living scattered across the country and keeping in touch by e-mail. They still come together during the holiday season and exchange gifts, but now setting up the gift exchange list presents a problem: At the beginning of each December when they lived together, each would draw a name from a bag to decide the one person to whom they would give a present that year. They can no longer do it that way because they won't meet until Christmas, and then it will be too late. The natural idea—appointing one of them to draw the names out of the bag, and informing each participant the name of the person whose gift they are to buy—is inconvenient for at least two reasons:
- The dwarf making the drawing would know who buys him a gift, which would spoil the surprise.
- There would be no guarantee of randomness: the dwarf setting up the exchange list could fabricate it instead of making a random draw. This is a difficulty because Grumpy and Doc are prone to complain.
Our December problem is to devise an e-mail equivalent of the random draw that would satisfy everybody. Set up a way for the dwarfs and Snow White to exchange information by e-mail so that
- No outside help from other persons or software is used;
- Everybody ends up with the name of the person for whom they are to buy a gift; everybody gets a gift, and everybody gives a gift.
- Nobody gets to know the name of the person buying his gift, and nobody can single handedly decide that person X buys a gift for person Y.
Perhaps your method may even improve on the paper bag: If a dwarf picks his own name from the bag, then they have to repeat the draw. Try to devise a method where such an occurrence is not possible. |
 Solution. Solution.
|
| PM90: November 2009 |
 | Consider a 4 by 4 grid of squares to be viewed as a crossword puzzle with four words across and four words down. In alphabetical order, seven of the eight words are
MPMM, OMPM, OMPP, OOMO, OOMP, POOM, and POPM.
What is the eighth word? |
 Solution. Solution.
|
| PM89: October 2009 |
 | A knockout tournament is a competition consisting of multiple rounds. In each round the competitors are paired up; the winner of each pairing moves on to the next round while the loser is eliminated. A bye is given to a competitor who has no assigned opponent, which means that he passes directly to the next round. We are interested in the minimum possible number of byes in a tournament having ncontestants. For example, when there are 6 contestants, the tournament might have two byes in the first round, or it can have no byes in the first round and just one bye in the second round. The minimum number of byes in a tournament having 6 contestants is therefore one.
- What is the minimum number of byes in a knockout tournament with 2010 contestants?
- Because of a doping scandal only 1025 contestants were able to compete in the tournament. How many byes did there have to be in the new draw?
|
 Solution. Solution.
|
| PM88: September 2009 |
 | The function f(x) satisfies two properties:
(i) f(x + y) + f(x - y) = 2[f(x) + f(y)], and
(ii) f(1) = 1.
What is f(22/7) ? |
 Solution. Solution.
|
|
|

No comments:
Post a Comment
Jika ada yang ingin disampaikan tentang isi blog ini, mohon kiranya berkenan untuk memberikan komentar di sini